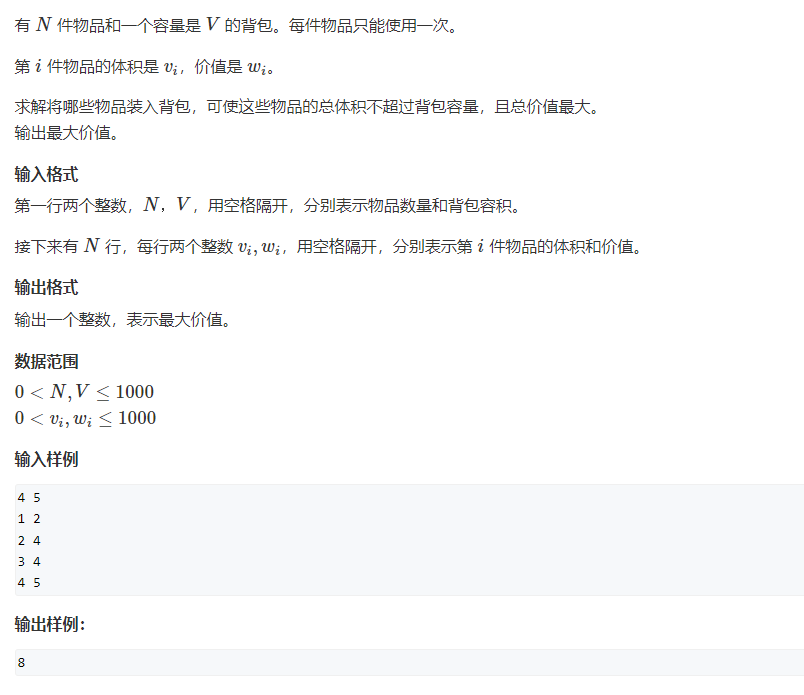
朴素版(二维)
- 状态f[i][j]定义:前 i 个物品,背包容量 j 下的最优解(最大价值):
当前的状态依赖于之前的状态,可以理解为从初始状态f[0][0] = 0开始决策,有 N 件物品,则需要 N 次决策,每一次对第 i 件物品的决策,状态f[i][j]不断由之前的状态更新而来。 - 当前背包容量不够(j < v[i]),没得选,因此前 i 个物品最优解即为前 i−1 个物品最优解:
对应代码:f[i][j] = f[i - 1][j]。 - 当前背包容量够,可以选,因此需要决策选与不选第 ii 个物品:
选:f[i][j] = f[i - 1][j - v[i]] + w[i]。
不选:f[i][j] = f[i - 1][j] 。
我们的决策是如何取到最大价值,因此以上两种情况取 max() 。
#include<iostream>
using namespace std;
const int N=1010;
int v[N],w[N],f[N][N];
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>v[i]>>w[i];
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
f[i][j]=f[i-1][j];
if(j>=v[i]){
f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
}
}
cout<<f[n][m]<<endl;
return 0;
}
优化版(一维)
- 由于f[i][j]表示装i个物品且体积为j的最大价值,那么在装第i个时只要保证前面i-1个的最大值装还是不装第i个,装就需要从i-1的个物品的总容量中-v[i]的体积,即f[i-1][j-v[i]],此时为不装i的最大价值,那么装上i之后,就需要+w[i], 则有f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i])。
- 那么去掉一维后,每次j都用上一次j-1的数据来更新,即f[j]取决于f[j-1]的值,我们for遍历时j是从小到大的,那么此时f[j-1]已经有值了,就不能再使用,所以我们逆序时,j是从大到小,此时可以使用f[j]=max(f[j],f[j-v[i]]+w[i]).
#include<iostream>
using namespace std;
const int N=1010;
int v[N],w[N],f[N];
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>v[i]>>w[i];
}
for(int i=1;i<=n;i++)
for(int j=m;j>=v[i];j--)
f[j]=max(f[j],f[j-v[i]]+w[i]);
cout<<f[m]<<endl;
return 0;
}
样例:
i=1,v[1]=1,w[1]=2时
f[5]=max(f[5],f[4]+2)=2
f[4]=max(f[4],f[3]+2)=2
f[3]=max(f[3],f[2]+2)=2
f[2]=max(f[2],f[1]+2)=2
f[1]=max(f[1],f[0]+2)=2
i=2,v[2]=2,w[2]=4时
f[5]=max(f[5],f[3]+4)=6
f[4]=max(f[4],f[2]+4)=6
f[3]=max(f[3],f[1]+4)=6
f[2]=max(f[2],f[0]+4)=4
f[1]=2
i=3,v[3]=3,w[3]=4时
f[5]=max(f[5],f[2]+4)=8
f[4]=max(f[4],f[1]+4)=6
f[3]=max(f[3],f[0]+2)=6
f[2]=4
f[1]=2
i=4,v[4]=4,w[4]=5时
f[5]=max(f[5],f[1]+5)=8
f[4]=max(f[4],f[0]+2)=6
f[3]=6
f[2]=4
f[1]=2
通过这个样例就很清楚为什么需要逆序,例如不逆序的话,f[1]更新之后才会算f[2],此时这个f[1]就不是上一轮的f[1]了。逆序之后,算f[2]用的上一次的f[1],就不会出现这种问题。
