acwing1237. 螺旋折线

题目

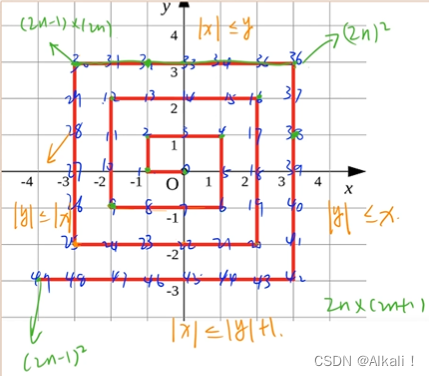
如下图所示的螺旋折线经过平面上所有整点恰好一次。

题解

#include<iostream>
using namespace std;
typedef long long LL;
LL distence=0;
int main(){
    int x,y;
    cin>>x>>y;
    if(y>=x&&y>=-x){//在上方
        int n=y;
        distence=(LL)(2*n)*(2*n-1)+x+n;
    }else if(y>=x&&y<=-x){//在左方
        int n=abs(x);
        distence=(LL)(2*n-1)*(2*n-1)+y-(-n+1);
    }else if(y<=x&&y>=-x){//在右方
        int n=x;
        distence=(LL)(2*n)*(2*n)+n-y;
    }else{
        int n=abs(y);
        distence=(LL)(2*n)*(2*n+1)+n-x;
    }
    cout<<distence<<endl;
    return 0;
    
}

找规律可以发现每层的右上角点所需步数为为4k²，求任意一个点的dis首先找到这个点所在的层数

• 如果在该层的左或上则减去该点到右上角曼哈顿距离，
• 如果在该层的右或下则加上该点到右上角曼哈顿距离；

#include<iostream>
using namespace std;
long long x,y;
int main(){
    cin>>x>>y;
    long long k=max(abs(x),abs(y));
    if(x>y)cout<<4*k*k+abs(x-k)+abs(y-k)<<endl;
    else cout<<4*k*k-abs(x-k)-abs(y-k)<<endl;
    return 0;
}