acwing100. 增减序列

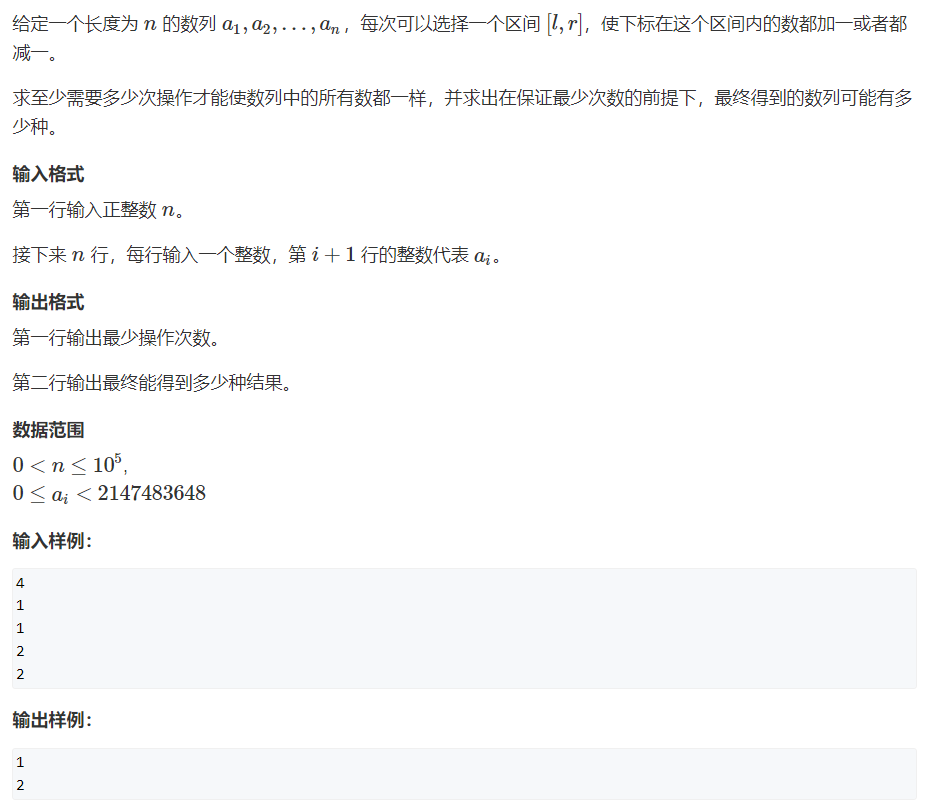
题目

题解

例如对于数列:1 1 2 2，得到的差分数列b[2_{n]=[0,1,0]，b从2开始因为b[1]=a[1]，由于差分的性质只需要将b[2}n]变为0，整个数列就是常数数列了。一般的差分数列正数负数都有，我们的目标很简单，就是将b[2~n]变为0。

每次操作我们都是选择一个区间进行加减，所以我们可以先将符号统一，例如全变成正数，此时只需要min（pos,neg)个操作，然后此时就全部是正数了，将正数变为0只需要：

1. b[1]和b[n+1]进行加减
2. b[i]和[b[n+1]进行加减

此时只需要abs(pos-neg)个操作就可以变为0.

对于得到多少种结果，取决于对b[1]的操作次数，只有abs(pos-neg)这一步需要对b[1]进行操作，可以选择操作也可以选择不操作（因为上面有两种方法，只有第一种才需要操作），所以有0~abs(pos-neg)中方法，即abs(pos-neg)+1

参考题解：https://www.yzlcoder.com/archives/3b534ab8.html

#include<iostream>
using namespace std;
const int N=1e5+10;
int n;
int a[N],b[N];

int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        b[i]=a[i]-a[i-1];
    }
    long long pos=0,neg=0;
    for(int i=2;i<=n;i++){
        if(b[i]>0)pos+=b[i];
        else neg-=b[i];
    }
    cout<<min(pos,neg)+abs(pos-neg)<<endl;
    cout<<abs(pos-neg)+1<<endl;
    
    
    return 0;
}